【理論】令和5年(下期) 問8|交流回路における共振時のインダクタンス電圧と共振周波数の関係に関する計算問題
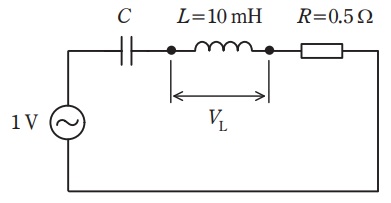
図のような交流回路において,電源の周波数を変化させたところ,共振時のインダクタンス \( L \) の端子電圧 \( V_L \) は \( 314 \) V であった。
共振周波数の値 [kHz] として,最も近いものを次の \( (1) \) ~ \( (5) \) のうちから一つ選べ。
合格への方程式
共振回路の基本概念
共振回路とは、コイル(L)とコンデンサ(C)を組み合わせた回路で、特定の周波数(共振周波数)で特殊な性質を示します。
共振状態では、コイルの誘導性リアクタンス(jωL)とコンデンサの容量性リアクタンス(1/jωC)が大きさが等しく逆符号になるため、互いに打ち消し合います。
共振回路には主に2種類あります:
- 直列共振回路:R、L、Cが直列に接続された回路
- 並列共振回路:R、L、Cが並列に接続された回路
どちらの回路でも共振周波数は同じ式で表されます:
\[ \begin{aligned} \omega_c = \frac{1}{\sqrt{LC}} \end{aligned} \]
周波数単位[Hz]では:
\[ \begin{aligned} f_c = \frac{1}{2\pi\sqrt{LC}} \end{aligned} \]
直列共振回路
直列共振回路では、R、L、Cが直列に接続されています。この回路の合成インピーダンスは:
\[ \begin{aligned} \dot{Z} &= R + j\omega L + \frac{1}{j\omega C} \\[10pt] &= R + j\left(\omega L - \frac{1}{\omega C}\right) \end{aligned} \]
合成インピーダンスは実部(抵抗成分)と虚部(リアクタンス成分)の和で表されます。
直列共振回路では、インピーダンスが最小になる周波数が共振周波数です。これは虚部が0になる条件から求められます:
\[ \begin{aligned} \omega_c L - \frac{1}{\omega_c C} &= 0 \\[10pt] \omega_c L &= \frac{1}{\omega_c C} \\[10pt] \omega_c^2 &= \frac{1}{LC} \\[10pt] \omega_c &= \frac{1}{\sqrt{LC}} \end{aligned} \]
直列共振回路の特徴:
- 共振時のインピーダンスは純抵抗(R)のみとなる
- 共振周波数で電流が最大になる
- 共振状態では電圧と電流が同相になる
並列共振回路
並列共振回路では、R、L、Cが並列に接続されています。この回路の合成アドミタンスは:
\[ \begin{aligned} \dot{Y} &= \frac{1}{R} + j\omega C + \frac{1}{j\omega L} \\[10pt] &= \frac{1}{R} + j\left(\omega C - \frac{1}{\omega L}\right) \end{aligned} \]
アドミタンスはインピーダンスの逆数であり、単位はジーメンス[S]です。
並列共振回路では、アドミタンスが最小(インピーダンスが最大)になる周波数が共振周波数です。これは虚部が0になる条件から求められます:
\[ \begin{aligned} \omega_c C - \frac{1}{\omega_c L} &= 0 \\[10pt] \omega_c C &= \frac{1}{\omega_c L} \\[10pt] \omega_c^2 &= \frac{1}{LC} \\[10pt] \omega_c &= \frac{1}{\sqrt{LC}} \end{aligned} \]
並列共振回路の特徴:
- 共振時のアドミタンスは純コンダクタンス(1/R)のみとなる
- 共振周波数で電流が最小になる
- 共振状態では電圧と電流が同相になる
- 高いインピーダンスを示すため「タンク回路」とも呼ばれる
共振回路の応用例
共振回路は多くの電子機器や通信システムで利用されています:
| 応用例 | 使用する共振回路 | 目的 |
|---|---|---|
| ラジオ受信機 | 並列共振回路 | 特定の周波数の信号を選択的に受信 |
| フィルタ回路 | 直列/並列共振回路 | 特定の周波数帯域の信号を通過/遮断 |
| 発振回路 | 並列共振回路 | 特定の周波数の信号を生成 |
| ワイヤレス充電 | 直列共振回路 | エネルギーを効率的に伝送 |
ラジオ受信機の同調回路
ワイヤレス充電システム
共振回路の Q 値(品質係数)は、回路の選択性と効率を表す重要な指標です。Q 値が高いほど、共振ピークが鋭くなり、特定の周波数をより精密に選択できます。
🔍 ワンポイントアドバイス: 直列共振回路と並列共振回路は、共振周波数では数式上は同じ形になりますが、回路動作は正反対です。直列回路は共振時にインピーダンスが最小(電流最大)、並列回路は共振時にインピーダンスが最大(電流最小)になることを覚えておきましょう。
今日はRLC直列共振回路について勉強するで!この回路は電気主任技術者試験でもよく出てくる重要な内容やからな。まずは基本的な直列共振回路の特徴について知ってるか?
はい、先生!RLC直列共振回路は、抵抗R、インダクタL、キャパシタCが直列に接続された回路です。この回路の特徴として、特定の周波数(共振周波数)において以下のような現象が起こります:
- インダクタのリアクタンスXLとキャパシタのリアクタンスXCが等しくなる
- XLとXCが互いに打ち消し合い、回路のインピーダンスが最小(抵抗Rのみ)になる
- 電流が最大になる
- インダクタとキャパシタの両端電圧が互いに180度位相がずれ、その大きさが等しくなる
おお、よう知ってるな!直列共振回路の特徴をしっかり理解してるやん。特に重要なのは、共振状態ではXLとXCが打ち消し合って、回路のインピーダンスが最小(R成分のみ)になるっていう点やな。
じゃあ、XLとXCが等しくなる条件、つまり共振条件の式を教えてくれるか?
はい、先生!共振条件はインダクタのリアクタンスXLとキャパシタのリアクタンスXCが等しくなることです。
インダクタのリアクタンスXLは:
\( X_L = 2\pi f_c L \)
キャパシタのリアクタンスXCは:
\( X_C = \frac{1}{2\pi f_c C} \)
共振条件はXL = XCなので:
\[ \begin{aligned} X_L &= X_C \\ 2\pi f_c L &= \frac{1}{2\pi f_c C} \\ (2\pi f_c)^2 LC &= 1 \\ f_c &= \frac{1}{2\pi \sqrt{LC}} \end{aligned} \]したがって、共振周波数fcは \( f_c = \frac{1}{2\pi \sqrt{LC}} \) という式で表されます。
さすがやな!共振周波数の式 \( f_c = \frac{1}{2\pi \sqrt{LC}} \) をしっかり導出できてるやん。これは第三種電気主任技術者試験でもよく出てくる重要な式やから、必ず覚えておいてな!
さて、実際に問題を解いていこか。ある直列共振回路があって、R = 0.5Ω、L = 10mH、共振時のインダクタ両端の電圧VL = 314Vやとする。この回路の共振周波数fcを求めてみよか。
まず、共振時の回路を流れる電流Iを考えてみよ。共振時の回路のインピーダンスはどうなるんやったかな?
はい、先生!共振時には、インダクタのリアクタンスXLとキャパシタのリアクタンスXCが打ち消し合うため、回路のインピーダンスZは抵抗Rのみになります。
つまり、共振時のインピーダンスZは:
\( Z = R = 0.5 \ \Omega \)
したがって、オームの法則より、共振時の電流Iは:
\[ \begin{aligned} I &= \frac{V}{Z} = \frac{V}{R} \\ &= \frac{1}{R} \cdot V \end{aligned} \]問題ではVの値が直接与えられていませんが、共振時にはインピーダンスが最小となるため、電源電圧を1Vと仮定すると、電流は:
\[ \begin{aligned} I &= \frac{1}{R} \\ &= \frac{1}{0.5} \\ &= 2 \ \mathrm{[A]} \end{aligned} \]となります。
よく考えられてるな!共振時には回路のインピーダンスが抵抗Rだけになって、Z = 0.5Ωになるんやね。電源電圧は問題に明示されてないけど、Vを1Vと仮定すると、I = V/R = 1/0.5 = 2Aとなる。実は電源電圧が何ボルトであっても、共振時の電流は2Aになるんや。
次に、インダクタの両端電圧VLを使って共振周波数fcを求めよう。インダクタの両端電圧VLと電流I、インダクタンスL、周波数fの関係式を思い出してみ?
はい、先生!インダクタの両端電圧VLと電流I、インダクタンスL、周波数fの関係式は次のようになります:
\[ V_L = 2\pi f L I \]または、インダクタのリアクタンスXLを使って:
\[ V_L = X_L \cdot I = 2\pi f L \cdot I \]この式を共振周波数fcについて解くと:
\[ \begin{aligned} V_L &= 2\pi f_c L I \\ f_c &= \frac{V_L}{2\pi L I} \end{aligned} \]この式に問題の値を代入します:
\[ \begin{aligned} f_c &= \frac{V_L}{2\pi L I} \\[10pt] &= \frac{314}{2\pi \times 10 \times 10^{-3} \times 2} \\[10pt] &= \frac{314}{0.4\pi \times 10^{-1}} \\[10pt] &= \frac{314 \times 10}{0.4\pi} \\[10pt] &= \frac{3140}{0.4\pi} \\[10pt] &\approx \frac{3140}{1.26} \\[10pt] &\approx 2500 \ \mathrm{[Hz]} \\[10pt] &= 2.5 \ \mathrm{[kHz]} \end{aligned} \]したがって、この回路の共振周波数fcは約2.5kHzです。
完璧や!計算もばっちりできてるな。共振周波数fcは2.5kHzと求められたわけやな。
確認のために、この共振周波数でのキャパシタの容量Cも計算してみよか。共振条件の式をC について解く必要があるな。
はい、先生!共振条件の式からキャパシタの容量Cを求めます。
共振周波数の式は:
\[ f_c = \frac{1}{2\pi \sqrt{LC}} \]これをCについて解きます:
\[ \begin{aligned} f_c &= \frac{1}{2\pi \sqrt{LC}} \\[10pt] 2\pi f_c &= \frac{1}{\sqrt{LC}} \\[10pt] (2\pi f_c)^2 &= \frac{1}{LC} \\[10pt] LC &= \frac{1}{(2\pi f_c)^2} \\[10pt] C &= \frac{1}{(2\pi f_c)^2 L} \end{aligned} \]ここに、fc = 2500Hz = 2.5kHz、L = 10mH = 0.01Hを代入します:
\[ \begin{aligned} C &= \frac{1}{(2\pi \times 2500)^2 \times 0.01} \\[10pt] &= \frac{1}{(5000\pi)^2 \times 0.01} \\[10pt] &= \frac{1}{25 \times 10^6 \times \pi^2 \times 0.01} \\[10pt] &= \frac{1}{25 \times 10^4 \times \pi^2} \\[10pt] &= \frac{10^4}{25 \times \pi^2} \times 10^{-6} \\[10pt] &\approx \frac{10^4}{25 \times 9.87} \times 10^{-6} \\[10pt] &\approx \frac{10^4}{246.75} \times 10^{-6} \\[10pt] &\approx 0.405 \times 10^{-6} \\[10pt] &\approx 0.405 \ \mathrm{[\mu F]} \end{aligned} \]したがって、この回路のキャパシタの容量Cは約0.405μFです。
よく計算できてるな!キャパシタの容量Cは約0.405μFとなるんやね。これで回路のすべてのパラメータが分かったわけや。
ところで、共振回路では、インダクタとキャパシタの両端電圧について面白い現象が起こるんやけど、知ってるか?
はい、先生!共振回路では、インダクタとキャパシタの両端電圧に関して興味深い現象が起こります。それは「電圧共振」と呼ばれる現象です。
具体的には:
- インダクタとキャパシタの両端電圧は互いに180度位相がずれています。つまり、一方が最大のとき、もう一方は最小になります。
- 共振時には、これらの電圧の大きさが等しくなります:VL = VC
- そして最も興味深いのは、これらの電圧が電源電圧よりもずっと大きくなることがあるという点です。これは「電圧増幅」または「Q倍」と呼ばれる現象です。
電圧の増幅率はQ(品質係数)に依存し、次の式で表されます:
\[ Q = \frac{X_L}{R} = \frac{X_C}{R} = \frac{2\pi f_c L}{R} = \frac{1}{2\pi f_c CR} \]共振時のインダクタやキャパシタの両端電圧は、電源電圧のQ倍になります:
\[ V_L = V_C = Q \times V \]Qが大きい(抵抗が小さい)回路では、インダクタやキャパシタの両端電圧が電源電圧の何倍にもなることがあり、これは回路設計時に注意すべき重要な点です。
素晴らしい!電圧共振についてもよく理解してるな。共振時には、インダクタとキャパシタの両端電圧がQ倍に増幅されるっていう現象は、実際の回路設計でめっちゃ重要なんや。
せっかくやから、今回の回路のQ値も計算してみよか。Q = XL/R = 2πfcL/R の式を使えばいいね。
はい、先生!Q値を計算します。
Q値の式は:
\[ Q = \frac{X_L}{R} = \frac{2\pi f_c L}{R} \]ここに、fc = 2500Hz、L = 10mH = 0.01H、R = 0.5Ωを代入します:
\[ \begin{aligned} Q &= \frac{2\pi \times 2500 \times 0.01}{0.5} \\[10pt] &= \frac{2\pi \times 25}{0.5} \\[10pt] &= \frac{50\pi}{0.5} \\[10pt] &= 100\pi \\[10pt] &\approx 314 \end{aligned} \]したがって、この回路のQ値は約314です。これは非常に高いQ値で、インダクタとキャパシタの両端電圧は電源電圧の約314倍にもなります。
実は、問題で与えられたインダクタの両端電圧VL = 314Vから、電源電圧が1Vであることが推測できます。なぜなら、VL = Q × V = 314 × 1 = 314Vとなるからです。
おお!すごいやん!Q = 314と計算して、さらにVL = 314Vから電源電圧が1Vやと推測したのはええ気づきやね!確かにVL = Q × Vの関係から、VL = 314V、Q = 314なら、V = 1Vになるわけや。
じゃあ、ちょっと別の角度から考えてみよか。今回の回路でインダクタとキャパシタの両端電圧はそれぞれいくらになるんやろう?
はい、先生!インダクタとキャパシタの両端電圧を計算します。
まず、インダクタの両端電圧VLは問題で与えられている通り:
\( V_L = 314 \ \mathrm{[V]} \)
共振時には、インダクタのリアクタンスXLとキャパシタのリアクタンスXCは等しくなります:
\( X_L = X_C \)
また、共振時の電流Iはすでに計算した通り2Aです。
キャパシタの両端電圧VCは:
\[ \begin{aligned} V_C &= X_C \times I \\[10pt] &= X_L \times I \ \ (\because X_L = X_C) \\[10pt] &= 2\pi f_c L \times I \\[10pt] &= 2\pi \times 2500 \times 0.01 \times 2 \\[10pt] &= 2\pi \times 25 \times 2 \\[10pt] &= 100\pi \\[10pt] &\approx 314 \ \mathrm{[V]} \end{aligned} \]したがって、キャパシタの両端電圧VCもインダクタの両端電圧VLと同じ314Vになります。ただし、両者は180度位相がずれているため、合成すると打ち消し合い、回路全体の電圧降下はR成分による電圧降下(1V)のみとなります。
完璧やな!計算も考え方も完全に理解できてるやん!VL = VC = 314Vで、お互いに180度位相がずれてるから打ち消し合う。だから回路全体の電圧降下はR成分による1Vだけになるんやね。
これが直列共振回路の面白いところで、電源電圧は1Vやのに、インダクタとキャパシタの両端には314Vもの高い電圧がかかるんや。これは実務上、絶縁設計などで注意せなあかん点やね。
さて、最後に直列共振回路の応用例について考えてみよか。どんなところで使われてると思う?
はい、先生!直列共振回路の応用例としては以下のようなものが挙げられます:
- 周波数選択回路(バンドパスフィルタ):特定の周波数だけを通過させるフィルタとして使用されます。ラジオやテレビの受信機などで、特定の放送局の信号だけを選択的に受信するために利用されます。
- 同調回路:特定の周波数で動作する回路の同調に使われます。例えば、無線通信機器の送受信部分や、電子楽器の音程制御などに応用されています。
- インピーダンスマッチング:電源と負荷のインピーダンスを整合させるために使用される場合があります。
- ノイズ除去回路:特定の周波数のノイズを除去するために使用されます。例えば、電源ラインのノイズフィルタなどに応用されています。
- 無線給電システム:最近では、スマートフォンのワイヤレス充電など、共振回路を利用した無線給電システムが実用化されています。
- 医療機器:MRI(磁気共鳴画像装置)などの医療機器でも、共振現象を利用した技術が応用されています。
これらの応用では、共振回路の特性、特に特定の周波数で選択的に応答する性質や、電圧増幅の特性が活用されています。
素晴らしい!直列共振回路の応用例をたくさん挙げてくれたね。特に周波数選択回路やノイズフィルタは、電気主任技術者として知っておくべき重要な応用やな。
今日は直列共振回路について学んだけど、振り返ってみると、次のようなポイントが重要やったね:
- 共振条件:XL = XCとなる周波数が共振周波数
- 共振周波数の式:\( f_c = \frac{1}{2\pi\sqrt{LC}} \)
- 共振時のインピーダンス:Z = R(最小値)
- 共振時の電流:I = V/R(最大値)
- Q値(品質係数):\( Q = \frac{X_L}{R} = \frac{X_C}{R} \)
- 電圧共振現象:VL = VC = Q×V
これらの知識は第三種電気主任技術者試験でも頻出やから、しっかり覚えておくんやで!
他に質問はあるかな?
はい、先生!一つ質問があります。今日は直列共振回路について学びましたが、並列共振回路というものもありますよね。直列共振回路と並列共振回路の違いや特徴について、簡単に教えていただけますか?
ええ質問やな!並列共振回路は直列共振回路と対をなす重要な回路やから、ちょっと説明しとこか。
並列共振回路(またはタンク回路とも呼ばれる)は、インダクタLとキャパシタCが並列に接続された回路や。直列共振回路との主な違いと特徴は次のようなものやね:
- 回路構成:LとCが並列に接続されている(直列共振回路はLとCが直列)
- 共振条件:直列共振と同じくXL = XCの条件で共振が起こる
- 共振周波数:理想的な場合(抵抗を無視した場合)は直列共振と同じく \( f_c = \frac{1}{2\pi\sqrt{LC}} \)
- インピーダンス特性:共振時にインピーダンスが最大になる(直列共振は最小)
- 電流特性:共振時に回路に流れる電流が最小になる(直列共振は最大)
- 電流共振:LとCの枝を流れる電流が互いに180度位相がずれていて、大きさが等しくなる。そのため、これらの電流は互いに打ち消し合い、電源から見ると小さな電流しか流れていないように見える。
- Q値の影響:Q値が高いほど、LとCの枝を流れる電流の増幅率が高くなる
応用例としては:
- バンドリジェクトフィルタ(特定の周波数を遮断するフィルタ)
- 発振回路(特に真空管やトランジスタの発振器)
- インピーダンス変換回路
- 電源回路の平滑化やノイズ除去
どうや?直列共振と並列共振の違いが分かったかな?
はい、先生!とてもわかりやすいご説明をありがとうございます。直列共振と並列共振の違いがよく理解できました。
特に印象的なのは、直列共振ではインピーダンスが最小になり電流が最大になるのに対して、並列共振ではインピーダンスが最大になり電流が最小になるという対照的な特徴ですね。また、直列共振では電圧共振が起こり、並列共振では電流共振が起こるという点も興味深いです。
実際の応用面でも、直列共振はバンドパスフィルタとして特定の周波数を通過させるのに使われ、並列共振はバンドリジェクトフィルタとして特定の周波数を遮断するのに使われるという対照的な使われ方をしているんですね。
今日の授業で、共振回路の基本的な理解が深まりました。ありがとうございました!
解説まとめ
直列共振時は回路のインピーダンスが最も小さくなり、抵抗分のみとなるため、回路を流れる電流 𝐼 [A] は次のように求まります:
\( I = \frac{1}{R} \)
\( = \frac{1}{0.5} \)
\( = 2 \ \mathrm{[A]} \)
したがって、共振時の電圧 \( V_{\mathrm{L}} = 314 \ \mathrm{[V]} \) より、共振周波数 \( f_{\mathrm{c}} \) [Hz] は以下の式で求められます:
\( V_{\mathrm{L}} = 2\pi f_{\mathrm{c}} L I \)
\( f_{\mathrm{c}} = \frac{V_{\mathrm{L}}}{2\pi L I} \)
\( = \frac{314}{2\pi \times 10 \times 10^{-3} \times 2} \)
\( \approx 2\ 500 \ \mathrm{[Hz]} \rightarrow 2.5 \ \mathrm{[kHz]} \)
このようにして、共振周波数は約 2.5 kHz と求められます。